Problem

Given an integer array nums, return true if any value appears at least twice in the array, and return false if every element is distinct.

Example 1:

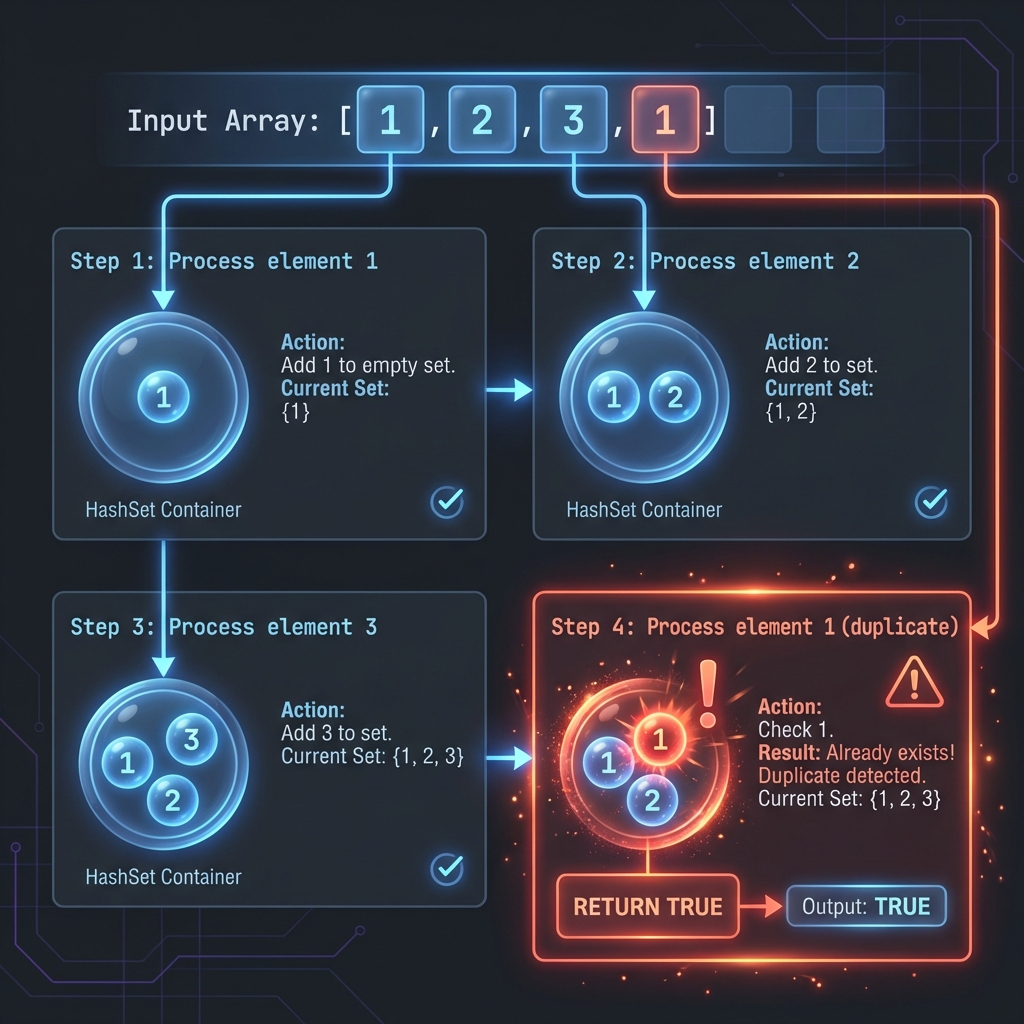
Input: nums = [1,2,3,1]
Output: true
Explanation: The element 1 occurs at the indices 0 and 3.

Example 2:

Input: nums = [1,2,3,4]
Output: false
Explanation: All elements are distinct.

Example 3:

Input: nums = [1,1,1,3,3,4,3,2,4,2]
Output: true

Constraints:

• 1 <= nums.length <= 10^5
• -10^9 <= nums[i] <= 10^9

---

Approach & Explanation

The optimal approach uses a HashSet to track elements we’ve seen:

1. Iterate through the array
2. For each element, check if it’s already in the set
3. If yes → return true (duplicate found)
4. If no → add it to the set
5. If we finish the loop without finding duplicates → return false

Complexity Analysis

• Time: O(n) - single pass through the array
• Space: O(n) - worst case, all elements are unique

Alternative Approaches

1. Sorting: Sort the array, then check adjacent elements. O(n log n) time, O(1) space.
2. Brute Force: Compare every pair. O(n²) time, O(1) space.

---

Solution

Java

import java.util.Set;
import java.util.HashSet;

class Solution {
    public boolean containsDuplicate(int[] nums) {
        Set<Integer> set = new HashSet<>();
        
        for(int num : nums) {
            if(set.contains(num)) {
                return true;
            }
            set.add(num);
        }

        return false;
    }
}

Go

func containsDuplicate(nums []int) bool {
    set := make(map[int]struct{}, len(nums))

    for _, num := range nums {
        if _, exists := set[num]; exists {
            return true
        }
        set[num] = struct{}{}
    }

    return false
}

---

Key Insight

The HashSet provides O(1) average time complexity for both contains() and add() operations, making this the most efficient solution for this problem.