Problem

Given a non-empty array of integers nums, every element appears twice except for one. Find that single one.

You must implement a solution with a linear runtime complexity and use only constant extra space.

Example 1:

Input: nums = [2,2,1]
Output: 1

Example 2:

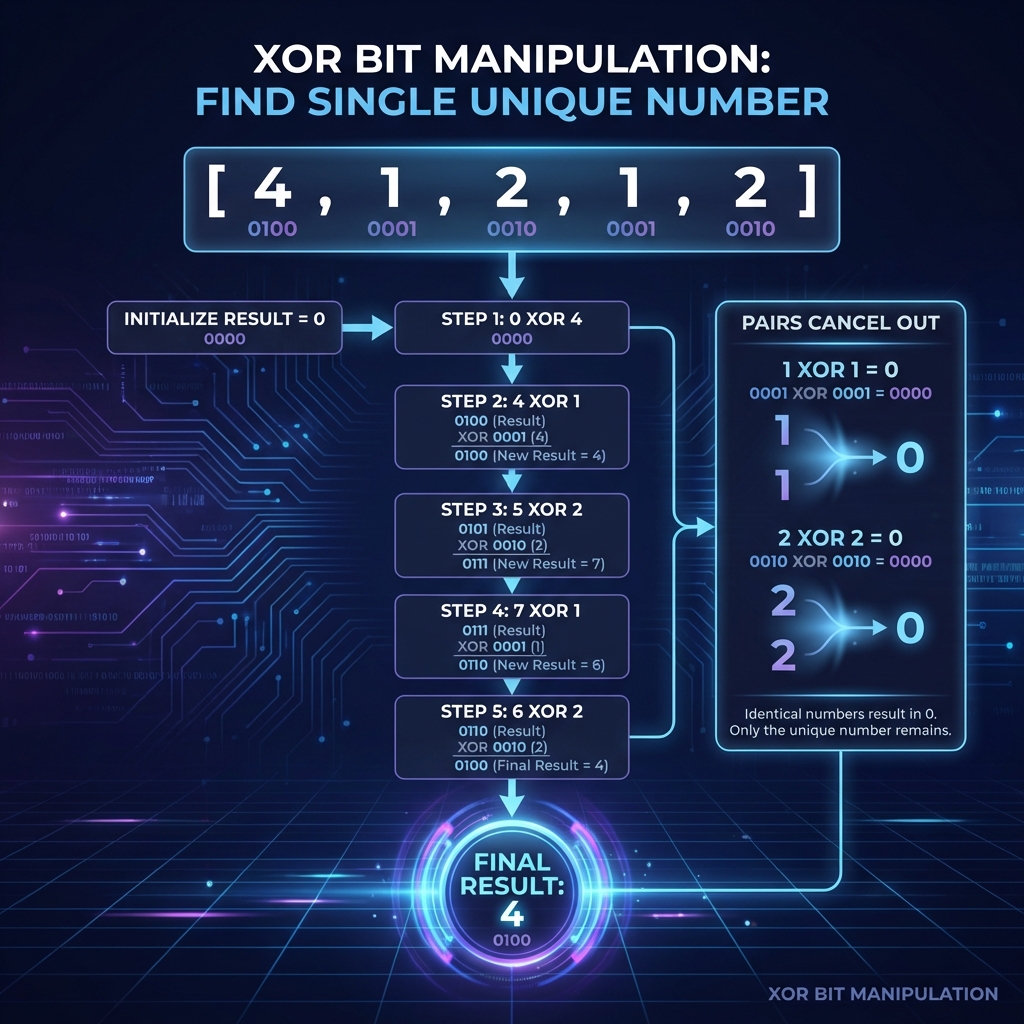
Input: nums = [4,1,2,1,2]
Output: 4

Example 3:

Input: nums = [1]
Output: 1

Constraints:

  • 1 <= nums.length <= 3 * 10^4
  • -3 * 10^4 <= nums[i] <= 3 * 10^4
  • Each element appears twice except for one element which appears only once.

Approach & Explanation

This is a classic problem that demonstrates the power of bit manipulation.

XOR Properties

The XOR (^) operator has these key properties:

  1. Self-cancellation: a ^ a = 0
  2. Identity: a ^ 0 = a
  3. Commutativity: a ^ b = b ^ a
  4. Associativity: (a ^ b) ^ c = a ^ (b ^ c)

Algorithm

If we XOR all numbers together:

  • Pairs cancel out: 2 ^ 2 = 0
  • The single number remains: 0 ^ 4 = 4

Example: [4, 1, 2, 1, 2]

4 ^ 1 ^ 2 ^ 1 ^ 2
= 4 ^ (1 ^ 1) ^ (2 ^ 2)
= 4 ^ 0 ^ 0
= 4

Complexity Analysis

  • Time: O(n) - single pass
  • Space: O(1) - only one variable

XOR Bit Manipulation Visualization

Solution

Java

class Solution {
    public int singleNumber(int[] nums) {
        int ans = 0;

        for(int num : nums) {
            ans ^= num;
        }

        return ans;
    }
}

Go

func singleNumber(nums []int) int {
    a := 0

    for _, num := range nums {
        a ^= num
    }

    return a
}

Key Insight

This problem perfectly meets the O(n) time and O(1) space constraints by leveraging the mathematical properties of XOR. This is a must-know pattern for bit manipulation problems!